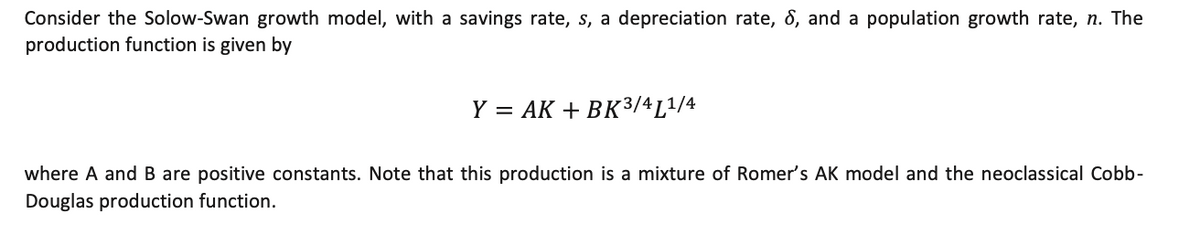
Extracted text: Consider the Solow-Swan growth model, with a savings rate, s, a depreciation rate, ô, and a population growth rate, n. The production function is given by Y = AK + BK3/4L1/4 where A and B are positive constants. Note that this production is a mixture of Romer's AK model and the neoclassical Cobb- Douglas production function.

Extracted text: • (i) Does this production function exhibit constant returns to scale? Explain why. • (ii) Does it exhibit diminishing returns to physical capital? Explain why. Y K • (ii) Express output per person, y =;, as a function of capital per person, k = ,. • (iv) Write down an expression for y/k as a function of k and graph. (Hint: as k goes to infinity, does the ratio y/k approach zero?) • (v) Use the production function in per capita terms to write the fundamental equation of the Solow-Swan model. • (vi) Suppose first that sA < 8="" +="" n.="" draw="" the="" savings="" curve="" and="" the="" depreciation="" curve,="" making="" sure="" to="" label="" the="" steady="" state="" level="" of="" capital(if="" it="" exists).="" what="" number="" does="" the="" savings="" curve="" approach="" as="" k="" goes="" to="" zero?="" as="" k="" goes="" to="" infinity,="" the="" savings="" curve="" approaches="" a="" number:="" what="" number="" is="" that?="" is="" it="" zero?="" •="" (vii)="" under="" these="" parameters,="" will="" there="" be="" positive="" growth="" in="" the="" long="" run?="" (remember="" that="" a="" and="" b="" are="" constants).="" why?="" •="" (viii)="" imagine="" that="" we="" have="" two="" countries="" with="" the="" same="" parameters="" (same="" a,="" b,="" s,="" 8,="" and="" n).="" one="" of="" them="" is="" rich="" and="" the="" other="" is="" poor.="" which="" one="" of="" the="" two="" will="" grow="" faster?="" why?="" will="" those="" two="" countries="" eventually="" catch="" up?="" •="" (ix)="" suppose="" now="" that="" sa=""> 8 + n. Draw the savings and depreciation curves, making sure to label the steady state level of capital(if it exists). Under these circumstances, will there be positive growth in the long run? Why? • (x) If s =0.4, A =2, B =1, 8 =.25, and n =0.10, the growth rate converges to some value as time goes to infinity. What is this value?