Consider the gambling game described in the St. Petersburg paradox, and assume that the utility function, U(x), for a change in fortune, x, is bounded, monotonically increasing on RI, and satisfies
 Show that the utility of playing the game is negative for a large enough cost c.
Show that the utility of playing the game is negative for a large enough cost c.
For which n in Example 3 is the expected utility positive?
An automobile company is about to introduce a new type of car into the market. It must decide how many of these new cars to produce. Let a denote the number of cars decided upon. A market survey will be conducted, with information obtained pertaining to (J, the proportion of the population which plans on buying a car and would tend to favor the new model. The company has determined that the major outside factor affecting the purchase of automobiles is the state of the economy. Indeed, letting Y denote an appropriate measure of the state of the economy, it is felt that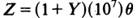
cars could be sold. Y is unknown, but is thought to have a OU(O, 1) distribution. Each car produced will be sold at a profit of $500, unless the supply (a) exceeds the demand (Z). If a > Z, the extra a - Z cars can be sold at a loss of $300 each. The company's utility function for money is linear (say U(rn) = rn) over the range involved. Determine L( (J, a). (The answer is
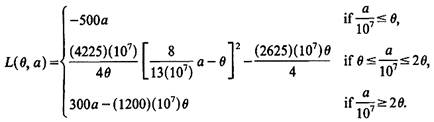
Note that in the middle region above, the loss is really a weighted squared-error loss, plus a term involving only (J.)