Consider the following game, which comes from James Andreoni and Hal Varian at the University of Michigan.19
A neutral referee runs the game. There are two players, Row and Column. The referee gives two cards to each: 2 and 7 to Row and 4 and 8 to Column. This is common knowledge. Then, playing simultaneously and independently, each player is asked to hand over to the referee either his high card or his low card. The referee hands out payoffs—which come from a central kitty, not from the players’
pockets—that are measured in dollars and depend on the cards that he collects. If Row chooses his Low card, 2, then Row gets $2; if he chooses his High card, 7, then Column gets $7. If Column chooses his Low card, 4, then Column gets $4; if he chooses his High card, 8, then Row gets $8.
(a) Show that the complete payoff table is as follows:
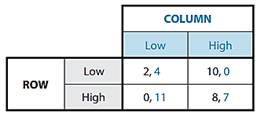
(b) What is the Nash equilibrium? Verify that this game is a prisoners’ dilemma.
Now suppose the game has the following stages. The referee hands out cards as before; who gets what cards is common knowledge. At stage I, each player, out of his own pocket, can hand over a sum of money, which the referee is to hold in an escrow account. This amount can be zero but cannot be negative. When both have made their stage I choices, these are publicly disclosed. Then at stage II, the two make their choices of cards, again simultaneously and independently. The referee hands out payoffs from the central kitty in the same way as in the single-stage game before. In addition, he disposes of the escrow account as follows. If Column chooses his high card, the referee hands over to Column the sum that Row put into the account; if Column chooses his low card, Row’s sum reverts back to him. The disposition of the sum that Column deposited depends similarly on Row’s card choice. All these rules are common knowledge.
(c) Find the rollback (subgame-perfect) equilibrium of this two-stage game. Does it resolve the prisoners’ dilemma? What is the role of the escrow account?