Consider the following demand and location data:
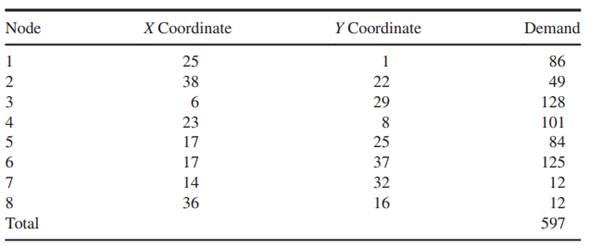
(a) Find the location of the 1-median for this problem using Manhattan distances. Give the value of the optimal objective function.
(b) Plot demands and the optimal facility location on an X–Y plot.
(c) Plot the contribution to the objective function of transportation (movement) in the X direction as we move the facility location in the
X direction from 0 to 40.
(d) Qualitatively and briefly discuss how the objective function and the optimal location would change if the coordinates of point 6 change from (17, 37) to (17, 100).
(e) We know that an optimal solution to this problem has an X coordinate equal to one of the X coordinates of the demand points. Call this= demand point node a for the sake of argument. Similarly, we know that the optimal location has a Y coordinate equal to one of the Y coordinates of the demand points. Call this demand point node b.
Note that nodes a and b need not be the same.
Now consider the same problem except that we are now restricted to selecting one of the demand nodes for the facility site. Consider the following conjecture:
Conjecture: An optimal solution to the 1-median problem using Manhattan distances must be at either node a or node b where node a is the node at which the demand-weighted distance in the X direction is minimized and node b is the node at which the demand-weighted distance in the Y direction is minimized.
Either prove that this conjecture is true or show by a counterexample that it is false.