Consider an economy involving three currencies. For i = 1, 2, 3, let
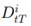
denote the value at time t of a zero coupon bond that pays a unit amount at T in currency i. Further, for i, j = 1, 2, 3, i = j, let
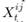
denote the value at time t in currency i of one unit of currency j, and let
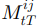
denote the corresponding forward FX rate at time t for maturity at T. Recall that
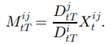
Suppose that a complete arbitrage-free model has been specified for the economy for the finite time interval
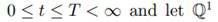
denote the EMM corresponding to numeraire
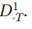
(i) Show that the time-zero value, stated in currency 2, of a call option that pays
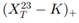
in currency 2 at time T can be expressed as
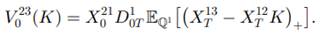
(ii) Suppose we are given the prices for all strikes of call options on
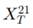
and
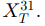
If the model is calibrated to these prices explain, using the expression in (i), what these prices tell us about the distributional information needed to calculate call prices on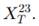
(iii) Let W∗ be a two-dimensional Brownian motion on the probability space (Ω, F,Q1) and let
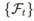
be the augmented natural filtration generated by W∗. Now suppose that under Q1
the processes
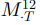
and
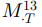
satisfy
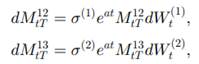
Where
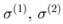
and a are positive constants and
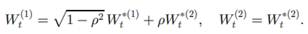
If Q2
denotes the EMM corresponding to numeraire
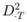
show that, under Q2,
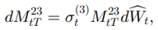
Where
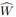
is an
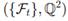
Brownian motion and
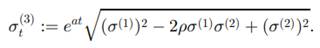
For this model derive an expression for
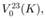
the time-zero value of the vanilla FX call option described in (i).