Consider a prototypical vibrations demonstration shown in Figure 10.11. In this demonstration, a rigid circular disk of mass m and radius R is attached at a point XS on its outer rim by a linear spring to a fixed point O. The spring is assumed to have
(a) Show that the kinetic energy of the disk has the following representation:
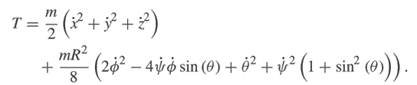
In addition, show that the potential energy of the disk has the representation
where the extension µ of the spring and the components of e3
are
(b) Show that the equations of motion for the disk can be expressed in the following form:
In these equations of motion, the mass matrix M is
We have refrained from expanding
in the interests of brevity.
(c) Prove that the total energy E = T + U of the disk is conserved by the solutions to the differential equations (10.69).
(d) Show that the determinant of the mass matrix is
Verify that the mass matrix becomes singular when the Euler basis
fails to be a basis for
E3.
(e) How would the equations of motion change if
were chosen instead of
