**coffee filter has mass 0.01908 kg
total stack mass m = 12 × 0.01908 = 0.22896 kg
AveVelInitial = y3 − y1/t3-t1 = 1.10446 m/s
t = 0 at the second observation of our collected data
distance fallen here is 0 m
initial velocity of 1.10446 m/s.
v(t) = (g−1/2m*ρACvo2)t+c
Where variables are
g is acceleration due to gravity
ρ is density of airC is drag coefficient
A is the cross sectional area of the object
vo is the initial velocit
m is mass of stacked coffee filters **
a) Solve your differential equation for v(t)
b) If you choose to solve the equation in v(t), the velocity, then you can integrate the velocity function you obtained, v(t), above to get position function
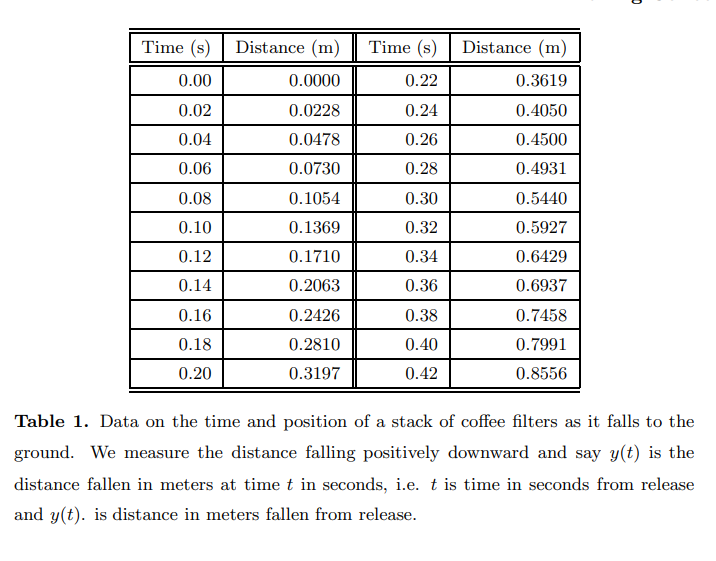
Extracted text: Time (s) Distance (m) Time (s) Distance (m) 0.00 0.0000 0.22 0.3619 0.02 0.0228 0.24 0.4050 0.04 0.0478 0.26 0.4500 0.06 0.0730 0.28 0.4931 0.08 0.1054 0.30 0.5440 0.10 0.1369 0.32 0.5927 0.12 0.1710 0.34 0.6429 0.14 0.2063 0.36 0.6937 0.16 0.2426 0.38 0.7458 0.18 0.2810 0.40 0.7991 0.20 0.3197 0.42 0.8556 Table 1. Data on the time and position of a stack of coffee filters as it falls to the ground. We measure the distance falling positively downward and say y(t) is the distance fallen in meters at time t in seconds, i.e. t is time in seconds from release and y(t). is distance in meters fallen from release.