choose 1 for each question:
a) (1, 2, 3 , 4 , 5)
b) (increase, decrease, or stay same)
c) (up or down)
d) (would change at y=1, would change at y= -1, would change at y= -3, would not change)
e) (would eventually approach y=1, would eventually approach y = -3, would eventually approach y = -4, would increase without bound, would decrease without bound)
f) (increase, decrease, or stay the same)
g) (up, down)
h) (would change at y=1, would change at y= -1, would change at y= -3, would not change)
i) (would eventually approach y=1, would eventually approach y= -3, would eventually approach y= -4, would increase without bound, would decrease without bound)
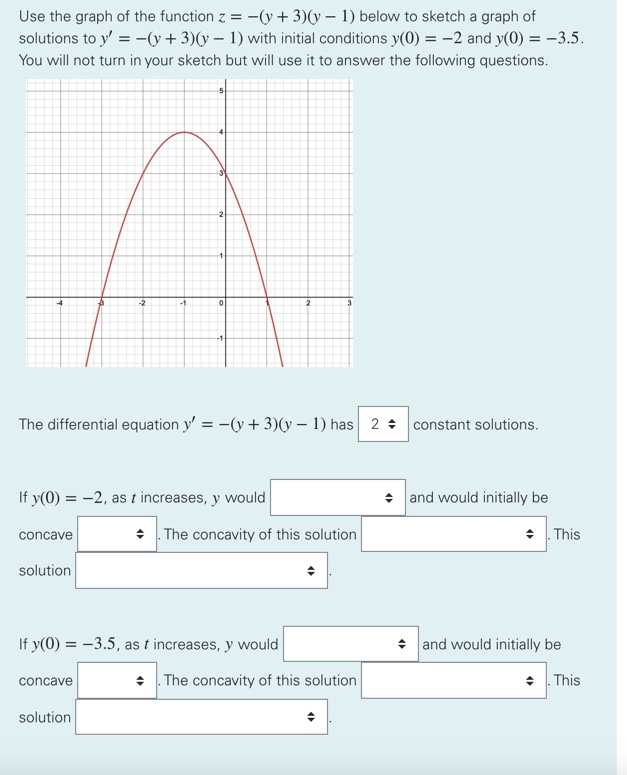
Extracted text: Use the graph of the function z = -(y + 3)(y – 1) below to sketch a graph of solutions to y' = -(y + 3)(y – 1) with initial conditions y(0) = -2 and y(0) = -3.5. You will not turn in your sketch but will use it to answer the following questions. -2 --1 The differential equation y' = -(y + 3)(y – 1) has 2 constant solutions. If y(0) = -2, as t increases, y would + and would initially be • The concavity of this solution + . This concave solution If y(0) = -3.5, as t increases, y would + and would initially be • . The concavity of this solution + . This concave solution