By appealing to show that
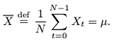
Note that the sample mean X is exactly equal to the parameter µ. Perfect estimation of model parameters rarely occurs in statistics: the simple model we are using here for pedagogical purposes has some special – and implausible – properties.
Since
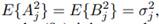
for a time series
that is a realization of a model given by (8a), it is natural to estimate Sj by
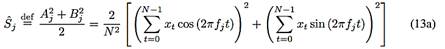
for 1 ≤ j <>
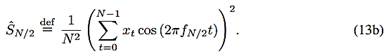
As examples of this estimation procedure, the thin curves in Figure 12 are graphs of Sˆ j versus fj
for the four time series in Figure 2. We can now see some justification for the theoretical spectra for these time series given previously (shown in these figures by the thick curves): the theoretical spectra are smoothed versions of the estimated spectra. Here are some points to note about the nonparametric spectral estimates. [1] Since Sˆ j involves just
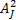
and
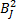
and since the Aj
and Bj
RVs are mutually uncorrelated, it can be argued that the Sˆj
RVs should be approximately uncorrelated (the assumption of Gaussianity for Aj
and Bj
makes this statement true without approximation). This property should be contrasted to that of the sample ACS, which is highly correlated for values with lags close to one another.
Letting
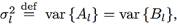
show that the harmonic process of Equation (35c) is a stationary process with mean µ and with an ACVS given by
If we compare Equations (35d) and (36a), we see that both the harmonic process and its ACVS consist of sums of cosine waves with exactly the same frequencies, but that all of the cosine terms are “in phase” for the ACVS; i.e., the φl RVs have been replaced by zeros. Note that the sequence {sτ} does not damp down to zero as τ gets large. Because
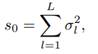
it follows that the ACS is given by
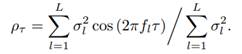
Let us consider two specific examples of harmonic processes. For the first example, we assume the RVs Al and Bl have a Gaussian distribution. Since a linear combination of Gaussian RVs is also a Gaussian RV, it follows from Equation (35c) that the resulting process {Xt} is a Gaussian stationary process. Recall that, if Y0, Y1, . . . , Yν−1
are independent zero mean, unit variance Gaussian RVs, then the RV
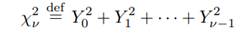
has a chi-square distribution with ν degrees of freedom. Since Al/σl and Bl/σl are independent zero mean, unit variance Gaussian RVs, it follows that
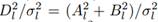
has a chi-square distribution with two degrees of freedom. The PDF for the RV
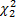
is given by
from which we can deduce that the PDF for
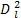
is given by
This is a special case of an exponential PDF f(u) = exp (−u/λ)/λ with a mean value of
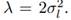
The random amplitude Dl is thus the square root of an exponential RV, which is said to obey a Rayleigh distribution. Anderson (1971, p. 376) notes that the symmetry of the bivariate Gaussian distribution for Al and Bl dictates that φ be uniformly distributed over the interval (−π, π] and be independent of Dl . Thus formulation of a Gaussian harmonic process via Equation (35d) involves Rayleigh distributed Dl and uniformly distributed φl , with all 2L RVs being independent of one another. Whereas a Gaussian-distributed harmonic process consists of random amplitudes and uniformly distributed random phases, our second example shows that we can dispense with the random amplitudes and still have a harmonic process.