An often used age-structured model of a population divides the number of females into age groups
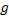
1,
, ··· ,
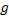
n
. Here
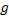
1
is the number in the youngest group,
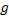
2
is the number in the second youngest group, etc. It is assumed that after a given time interval,
i
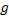
i
of those in
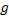
i
survive and move to age group
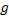
i+1. Also, over the same time interval, the females in
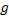
i
produce bigi female babies. Setting
g
= (
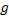
1,
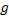
2, ··· ,
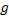
n
)
T
, with
gk being the value at time step
k
and
g
k+1
being the value at time step
k+1
, then
g
k+1
=
Ag
k
, where
This is known as a Leslie matrix. It is assumed that the
i
’s are positive,
1
and
n
are non-negative, and the other
i
’s are positive. In this case, the dominant eigenvalue λ1
of
A
is positive. If λ1
> 1, then the population increases, and it decreases if λ1
<>
linearly independent eigenvectors.
(a) Deer can survive up to 20 years in the wild. Taking
= 20, and assuming their survivability deceases with age, let
i
= exp(−
/100). Also, assuming 3/4 of the females in each age group have one offspring each year, with equal probability of being male or female, then
i
= (3/4)(1/2) = 3/8. The exception is the youngest group, and for this assume that
1
= 0. Does the population increase or decrease?
(b) If λ1
= 1, then the population approaches a constant value as time increases. For the deer in part (a), assuming
1
= 0 and
2
=
3
= ··· =
n
=
, what does
have to be so this happens? The value you find should be correct to six significant digits.