After one month of the season, eleven baseball players have batting averages of 0.240, 0.310, 0.290, 0.180, 0.285, 0.240, 0.370, 0.255, 0.290, 0.260, and 0.210. It is desired to estimate the year-end batting average, OJ, of each player; the one month batting averages, X;, can be assumed to be K(Oj, (0.03)2) random variables. The previous year's batting averages of the eleven players were 0.220, 0.280, 0.320, 0.280, 0.260, 0.280, 0.300, 0.240, 0.310, 0.240, and 0.240, respectively. These can be considered to be prior means for this year's OJ, and it is known that the yearly variation of a player's average tends to be about 0.02 (which can be considered to be the prior standard deviations).
(a) Assuming a conjugate normal prior, calculate the posterior means and variances for the
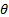
i.
(b) Using the robust prior of Subsection 4.7.10, calculate the posterior means and variances for the
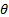
i.
(c) Suppose a few extreme conflicts, between the Xi and the prior means, will sometimes occur in this scenario. Perform a type of robust Bayes analysis which protects against this possibility.
151. In Example 55, verify that any randomized action can be dominated by an action in the interval [0.75,0.79].