A weight (W)is dropped from a height (y) upon the cantilever beam in Fig. P7.17 causing a permanent deformation (δ), where δ is a function of h, b, ﻠ, and σ f in addition to W and y (where σ f is the...

A weight (W)is dropped from a height (y) upon the cantilever beam in Fig. P7.17 causing a permanent deformation (δ), where δ is a function of h, b, ﻠ, and σ_f
in addition to W and y (where σ_f
is the plastic flow stress of the beam material). Thus, before dimensional analysis:

               δ = ψ₃
(W, y, h, b, ﻠ, σ_f)

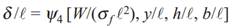
However, further reflection reveals that in place of W and y, the energy of impact (U = Wy) may be used, and instead of h and b, the moment of inertia about the neutral axis (IN) = 1/12 bh³
[in.4] may be employed. Starting over:

                  δ = ψ₃
(U, IN, ﻠ, σ_f)

a) Perform a dimensional analysis.

b) When a 1:10 scale model test is performed under geometrically similar conditions where σ_p/σ_m
= 2, it is found that when Um = 10 in. lbs, δ_m
= 0.1 inch. Find the corresponding values of Up and δ_p.