A researcher wants to see if gender and/or income affect the total amount of help given to a stranger who is sitting on the side of a busy road with a sign asking for help.
The independent variables are gender, income, and the interaction of gender and income.
The dependent variable is total help.
He wants to know if one or both factors – or the interaction of the two - affect the total amount of help offered. Because he is analyzing two independent variables (gender and income), he used a factorial ANOVA. His results show the main effect of each of the independent variables on the dependent variable (total help) and the interaction effect. The researcher is using a 95% confidence interval which means that he wants to be at least 95% sure that his independent variables affected total help if he rejects the null hypothesis.
What is one research hypothesis (there are three possible hypotheses here name them all if you can but naming at least one is required)?
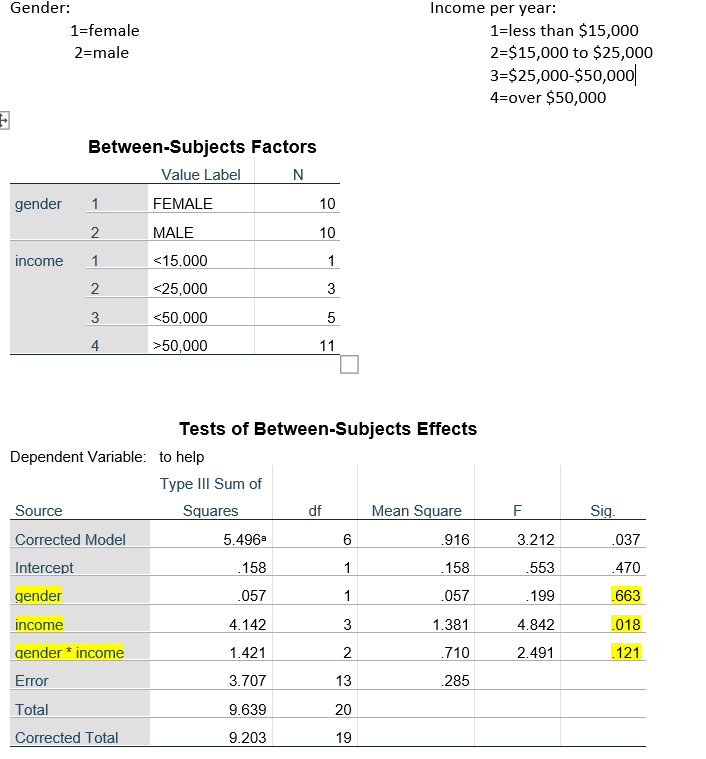
Extracted text: Gender: Income per year: 1=less than $15,000 2=$15,000 to $25,000 3-$25,000-$50,00o| 4=over $50,000 1=female 2=male Between-Subjects Factors Value Label N gender 1 FEMALE 10 MALE 10 income 1 <15.000 1=""><25,000 3="" 3=""><50.000 5="" 4="">50,000 11 Tests of Between-Subjects Effects Dependent Variable: to help Type III Sum of Source Squares df Mean Square F Sig. Corrected Model 5.496 .916 3.212 .037 Intercept .158 1 .158 .553 470 gender .057 1 .057 .199 663 income 4.142 1.381 4.842 018 gender * income 1.421 2 .710 2.491 121 Error 3.707 13 .285 Total 9.639 20 Corrected Total 9.203 19 CO 3.
Extracted text: gender age marital ethnic income tothelp hseveret problem 1 1 22 2 4 4 -45 4.0 2 24 1 3 43 5.0 3 1 39 2 1 3 .63 6.7 1 4. 2 42 1 4 -98 4.0 3 1 29 1 1 4 .87 4.5 3 6 1 22 1 1 -20 3.5 1 7 26 1 4 -.06 2.0 1 8 2 60 2 1 4 -.98 5.0 3 9 2 28 2 2 1.59 7.0 1 10 1 37 1 1 1.01 4.0 2 11 1 43 1 1 32 6.0 12 1 39 1 3 .12 7.0 2 13 2 27 2 2 4 .15 5.0 2 14 2 45 1 1 4 .39 6.5 2 15 1 54 1 1 4 .65 5.5 3 16 77 1 1 -.11 7.0 1 17 1 33 2 1 2 .16 7.0 2 18 1 33 1 1 47 5.0 19 2 25 1 1 -1.25 2.5 1 20 2 38 1 4 .16 5.0 21 2. 3. 4. 3. 3. 2. 24 3. 2. 2. 2. 2. 2. 5. CO