A research team is working on a project to study the time (in seconds) for high school male runners to finish a 400-meter race. Jimmy, a junior researcher in the team, has randomly selected a sample...


A research team is working on a project to study the time (in seconds) for high school male runners to finish
a 400-meter race. Jimmy, a junior researcher in the team, has randomly selected a sample of 25 male runners
from a high school and the time (in seconds) for each of them to complete a 400-meter race was recorded.
The sample mean running time was 53 seconds. It is assumed that the running time in a 400-meter race
follows a normal distribution with a population standard deviation of 5.5 seconds.
(a) Give a point estimate of the population mean running time for a 400-meter race.
(b) Calculate the sampling error at 95% confidence level.
(c) Construct a 95% confidence interval estimate of the population mean running time for a 400-meter race.


(d) If instead of 25, 80 male runners are selected for the study, what is the sampling error at 95% confidence
level? When the 95% confidence interval is constructed based on a sample with 80 male runners, would
you expect the interval will be (I) narrower, (II) wider, or (III) the same width as the confidence interval
constructed in part (c)?
(e) After discussion with the research director, Jimmy is asked to work on the research again. This time,
he needs to ensure the difference between the point estimate and the true population mean be within
± 0.8 seconds at 99% confidence level. To fulfil the requirement, how large should be the minimum
sample size?




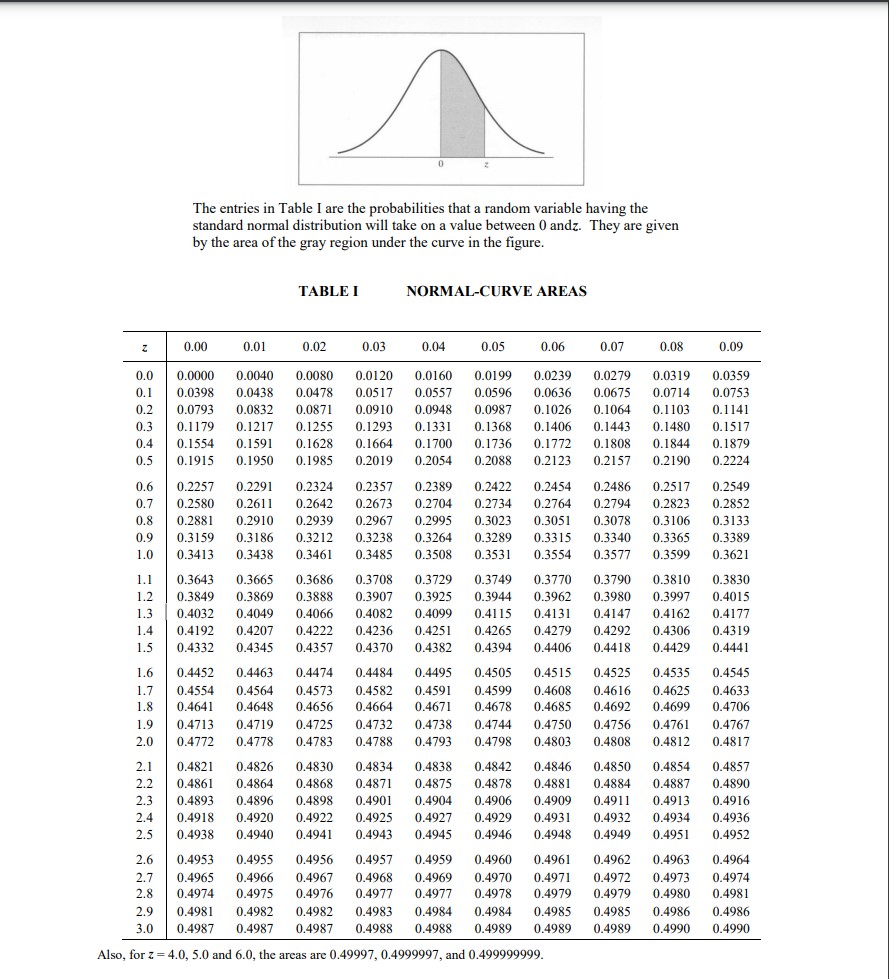
The entries in Table I are the probabilities that a random variable having the<br>standard normal distribution will take on a value between 0 andz. They are given<br>by the area of the gray region under the curve in the figure.<br>TABLE I<br>NORMAL-CURVE AREAS<br>0.00<br>0.01<br>0.02<br>0.03<br>0.04<br>0.05<br>0.06<br>0.07<br>0.08<br>0.09<br>0.0<br>0.0000<br>0.0040<br>0.0080<br>0.0120<br>0.0160<br>0.0199<br>0.0239<br>0.0279<br>0.0319<br>0.0359<br>0.1<br>0.0398<br>0.0438<br>0.0478<br>0.0517<br>0.0557<br>0.0596<br>0.0636<br>0.0675<br>0.0714<br>0.0753<br>0.2<br>0.0793<br>0.0832<br>0.0871<br>0.0910<br>0.0948<br>0.0987<br>0.1026<br>0.1064<br>0.1103<br>0.1141<br>0.3<br>0.1179<br>0.1217<br>0.1255<br>0.1293<br>0.1331<br>0.1368<br>0.1406<br>0.1443<br>0.1480<br>0.1517<br>0.4<br>0.1554<br>0.1591<br>0.1628<br>0.1664<br>0.1700<br>0.1736<br>0.1772<br>0.1808<br>0.1844<br>0.1879<br>0.5<br>0.1915<br>0.1950<br>0.1985<br>0.2019<br>0.2054<br>0.2088<br>0.2123<br>0.2157<br>0.2190<br>0.2224<br>0.6<br>0.2257<br>0.2291<br>0.2324<br>0.2357<br>0.2389<br>0.2422<br>0.2454<br>0.2486<br>0.2517<br>0.2549<br>0.7<br>0.2580<br>0.2611<br>0.2642<br>0.2673<br>0.2704<br>0.2734<br>0.2764<br>0.2794<br>0.2823<br>0.2852<br>0.8<br>0.2881<br>0.2910<br>0.2939<br>0.2967<br>0.2995<br>0.3023<br>0.3051<br>0.3078<br>0.3106<br>0.3133<br>0.9<br>0.3159<br>0.3186<br>0.3212<br>0.3238<br>0.3264<br>0.3289<br>0.3315<br>0.3340<br>0.3365<br>0.3389<br>1.0<br>0.3413<br>0.3438<br>0.3461<br>0.3485<br>0.3508<br>0.3531<br>0.3554<br>0.3577<br>0.3599<br>0.3621<br>1.1<br>0.3643<br>0.3665<br>0.3686<br>0.3708<br>0.3729<br>0.3749<br>0.3770<br>0.3790<br>0.3810<br>0.3830<br>0.3907<br>0.4082<br>1.2<br>0.3849<br>0.3869<br>0.3888<br>0.3925<br>0.3944<br>0.3962<br>0.3980<br>0.3997<br>0.4015<br>1.3<br>0.4032<br>0.4049<br>0.4066<br>0.4099<br>0.4115<br>0.4131<br>0.4147<br>0.4162<br>0.4177<br>1.4<br>0.4192<br>0.4207<br>0.4222<br>0.4236<br>0.4251<br>0.4265<br>0.4279<br>0.4292<br>0.4306<br>0.4319<br>1.5<br>0.4332<br>0.4345<br>0.4357<br>0.4370<br>0.4382<br>0.4394<br>0.4406<br>0.4418<br>0.4429<br>0.4441<br>1.6<br>0.4452<br>0.4463<br>0.4474<br>0.4484<br>0.4495<br>0.4505<br>0.4515<br>0.4525<br>0.4535<br>0.4545<br>0.4573<br>0.4656<br>0.4582<br>0.4664<br>0.4591<br>0.4671<br>0.4599<br>0.4678<br>0.4608<br>0.4685<br>0.4625<br>0.4699<br>0.4633<br>0.4706<br>1.7<br>0.4554<br>0.4564<br>0.4616<br>1.8<br>0.4641<br>0.4648<br>0.4692<br>1.9<br>0.4713<br>0.4719<br>0.4725<br>0.4732<br>0.4738<br>0.4744<br>0.4750<br>0.4756<br>0.4761<br>0.4767<br>2.0<br>0.4772<br>0.4778<br>0.4783<br>0.4788<br>0.4793<br>0.4798<br>0.4803<br>0.4808<br>0.4812<br>0.4817<br>2.1<br>0.4821<br>0.4826<br>0.4830<br>0.4834<br>0.4838<br>0.4842<br>0.4846<br>0.4850<br>0.4854<br>0.4857<br>2.2<br>0.4861<br>0.4864<br>0.4868<br>0.4871<br>0.4875<br>0.4878<br>0.4881<br>0.4884<br>0.4887<br>0.4890<br>2.3<br>0.4893<br>0.4896<br>0.4898<br>0.4901<br>0.4904<br>0.4906<br>0.4909<br>0.4911<br>0.4913<br>0.4916<br>2.4<br>0.4918<br>0.4920<br>0.4922<br>0.4925<br>0.4927<br>0.4929<br>0.4931<br>0.4932<br>0.4934<br>0.4936<br>2.5<br>0.4938<br>0.4940<br>0.4941<br>0.4943<br>0.4945<br>0.4946<br>0.4948<br>0.4949<br>0.4951<br>0.4952<br>2.6<br>0.4953<br>0.4955<br>0.4956<br>0.4957<br>0.4959<br>0.4960<br>0.4961<br>0.4962<br>0.4963<br>0.4964<br>0.4965<br>0.4974<br>0.4969<br>0.4977<br>0.4971<br>0.4979<br>0.4973<br>0.4980<br>2.7<br>0.4966<br>0.4967<br>0.4968<br>0.4970<br>0.4972<br>0.4974<br>2.8<br>0.4975<br>0.4976<br>0.4977<br>0.4978<br>0.4979<br>0.4981<br>0.4984<br>0.4988<br>2.9<br>0.4981<br>0.4982<br>0.4982<br>0.4983<br>0.4984<br>0.4985<br>0.4985<br>0.4986<br>0.4986<br>3.0<br>0.4987<br>0.4987<br>0.4987<br>0.4988<br>0.4989<br>0.4989<br>0.4989<br>0.4990<br>0.4990<br>Also, for z = 4.0, 5.0 and 6.0, the areas are 0.49997, 0.4999997, and 0.499999999.<br>

Extracted text: The entries in Table I are the probabilities that a random variable having the standard normal distribution will take on a value between 0 andz. They are given by the area of the gray region under the curve in the figure. TABLE I NORMAL-CURVE AREAS 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359 0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753 0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141 0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517 0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879 0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224 0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549 0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852 0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133 0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389 1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621 1.1 0.3643 0.3665 0.3686 0.3708 0.3729 0.3749 0.3770 0.3790 0.3810 0.3830 0.3907 0.4082 1.2 0.3849 0.3869 0.3888 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015 1.3 0.4032 0.4049 0.4066 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177 1.4 0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319 1.5 0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441 1.6 0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545 0.4573 0.4656 0.4582 0.4664 0.4591 0.4671 0.4599 0.4678 0.4608 0.4685 0.4625 0.4699 0.4633 0.4706 1.7 0.4554 0.4564 0.4616 1.8 0.4641 0.4648 0.4692 1.9 0.4713 0.4719 0.4725 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767 2.0 0.4772 0.4778 0.4783 0.4788 0.4793 0.4798 0.4803 0.4808 0.4812 0.4817 2.1 0.4821 0.4826 0.4830 0.4834 0.4838 0.4842 0.4846 0.4850 0.4854 0.4857 2.2 0.4861 0.4864 0.4868 0.4871 0.4875 0.4878 0.4881 0.4884 0.4887 0.4890 2.3 0.4893 0.4896 0.4898 0.4901 0.4904 0.4906 0.4909 0.4911 0.4913 0.4916 2.4 0.4918 0.4920 0.4922 0.4925 0.4927 0.4929 0.4931 0.4932 0.4934 0.4936 2.5 0.4938 0.4940 0.4941 0.4943 0.4945 0.4946 0.4948 0.4949 0.4951 0.4952 2.6 0.4953 0.4955 0.4956 0.4957 0.4959 0.4960 0.4961 0.4962 0.4963 0.4964 0.4965 0.4974 0.4969 0.4977 0.4971 0.4979 0.4973 0.4980 2.7 0.4966 0.4967 0.4968 0.4970 0.4972 0.4974 2.8 0.4975 0.4976 0.4977 0.4978 0.4979 0.4981 0.4984 0.4988 2.9 0.4981 0.4982 0.4982 0.4983 0.4984 0.4985 0.4985 0.4986 0.4986 3.0 0.4987 0.4987 0.4987 0.4988 0.4989 0.4989 0.4989 0.4990 0.4990 Also, for z = 4.0, 5.0 and 6.0, the areas are 0.49997, 0.4999997, and 0.499999999.
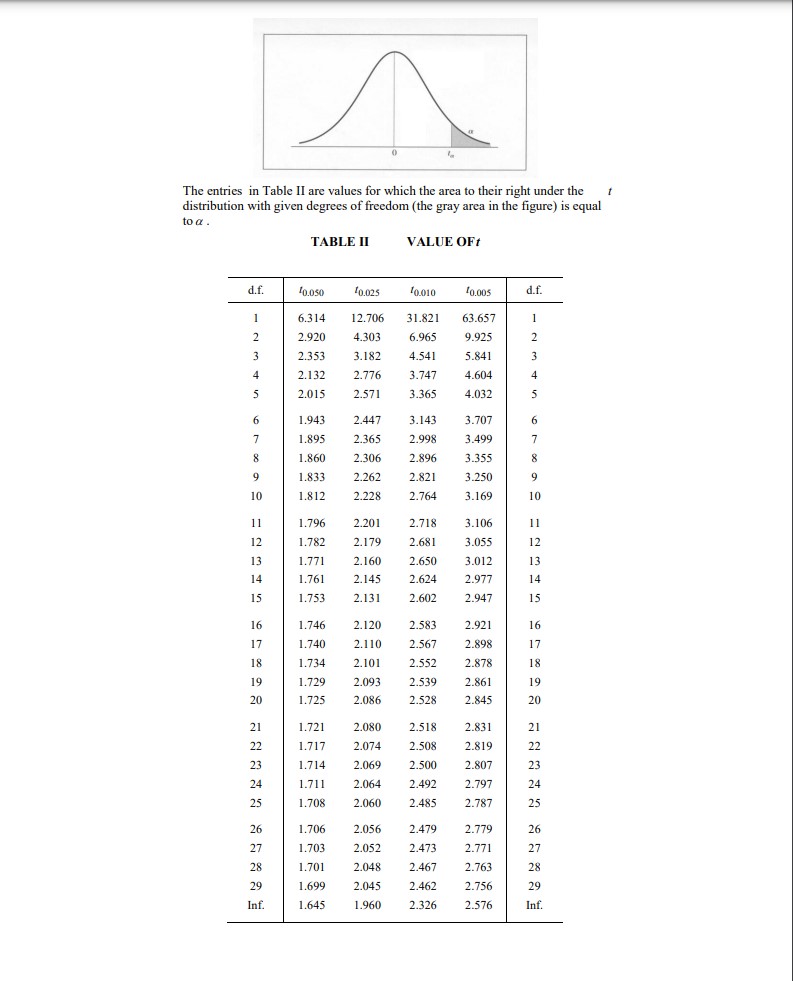
The entries in Table II are values for which the area to their right under the<br>distribution with given degrees of freedom (the gray area in the figure) is equal<br>to a.<br>TABLE II<br>VALUE OFt<br>d.f.<br>'0.0s0<br>l0.025<br>f0.010<br>10.005<br>d.f.<br>1<br>6.314<br>12.706<br>31.821<br>63.657<br>1<br>2.920<br>4.303<br>6.965<br>9.925<br>3<br>2.353<br>3.182<br>4.541<br>5.841<br>3<br>4<br>2.132<br>2.776<br>3.747<br>4.604<br>4<br>5<br>2.015<br>2.571<br>3.365<br>4.032<br>5<br>6.<br>1.943<br>2.447<br>3.143<br>3.707<br>6.<br>1.895<br>2.365<br>2.998<br>3.499<br>7<br>8<br>1.860<br>2.306<br>2.896<br>3.355<br>8.<br>9<br>1.833<br>2.262<br>2,821<br>3.250<br>9<br>10<br>1.812<br>2.228<br>2.764<br>3.169<br>10<br>11<br>1.796<br>2.201<br>2.718<br>3.106<br>11<br>12<br>1.782<br>2.179<br>2.681<br>3.055<br>12<br>13<br>1.771<br>2.160<br>2.650<br>3.012<br>13<br>14<br>1.761<br>2.145<br>2.624<br>2.977<br>14<br>15<br>1.753<br>2.131<br>2.602<br>2.947<br>15<br>16<br>1.746<br>2.120<br>2.583<br>2.921<br>16<br>17<br>1.740<br>2.110<br>2.567<br>2.898<br>17<br>18<br>1.734<br>2.101<br>2.552<br>2.878<br>18<br>19<br>1.729<br>2.093<br>2.539<br>2.861<br>19<br>20<br>1.725<br>2.086<br>2.528<br>2.845<br>20<br>21<br>1.721<br>2,080<br>2.518<br>2.831<br>21<br>22<br>1.717<br>2.074<br>2.508<br>2.819<br>22<br>23<br>1.714<br>2.069<br>2.500<br>2.807<br>23<br>24<br>1.711<br>2.064<br>2.492<br>2.797<br>24<br>25<br>1.708<br>2.060<br>2.485<br>2.787<br>25<br>26<br>1.706<br>2.056<br>2.479<br>2.779<br>26<br>27<br>1.703<br>2.052<br>2.473<br>2.771<br>27<br>28<br>1.701<br>2.048<br>2.467<br>2.763<br>28<br>29<br>1.699<br>2.045<br>2.462<br>2.756<br>29<br>Inf.<br>1.645<br>1.960<br>2.326<br>2.576<br>Inf.<br>

Extracted text: The entries in Table II are values for which the area to their right under the distribution with given degrees of freedom (the gray area in the figure) is equal to a. TABLE II VALUE OFt d.f. '0.0s0 l0.025 f0.010 10.005 d.f. 1 6.314 12.706 31.821 63.657 1 2.920 4.303 6.965 9.925 3 2.353 3.182 4.541 5.841 3 4 2.132 2.776 3.747 4.604 4 5 2.015 2.571 3.365 4.032 5 6. 1.943 2.447 3.143 3.707 6. 1.895 2.365 2.998 3.499 7 8 1.860 2.306 2.896 3.355 8. 9 1.833 2.262 2,821 3.250 9 10 1.812 2.228 2.764 3.169 10 11 1.796 2.201 2.718 3.106 11 12 1.782 2.179 2.681 3.055 12 13 1.771 2.160 2.650 3.012 13 14 1.761 2.145 2.624 2.977 14 15 1.753 2.131 2.602 2.947 15 16 1.746 2.120 2.583 2.921 16 17 1.740 2.110 2.567 2.898 17 18 1.734 2.101 2.552 2.878 18 19 1.729 2.093 2.539 2.861 19 20 1.725 2.086 2.528 2.845 20 21 1.721 2,080 2.518 2.831 21 22 1.717 2.074 2.508 2.819 22 23 1.714 2.069 2.500 2.807 23 24 1.711 2.064 2.492 2.797 24 25 1.708 2.060 2.485 2.787 25 26 1.706 2.056 2.479 2.779 26 27 1.703 2.052 2.473 2.771 27 28 1.701 2.048 2.467 2.763 28 29 1.699 2.045 2.462 2.756 29 Inf. 1.645 1.960 2.326 2.576 Inf.

Jun 04, 2022
SOLUTION.PDF
SOLUTION.PDF

Get Answer To This Question

Related Questions & Answers

More Questions »

Submit New Assignment

Copy and Paste Your Assignment Here
Have files?