(a) Consider the map
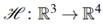
defined such that
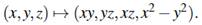
Prove that when it is restricted to the sphere S2 (inR3), we have H (x,y,z) = H (x′,y′,z′) iff (x′,y′,z′)=(x,y,z)or(x′,y′,z′)=(−x,−y,−z). In other words, the inverse image of every point in H(S2) consists of two anti podal points. Prove that the map Hinducesan injective map from the projective plane onto H(S2), and that iti saho meomor phism. (b)The map Hallow sustore alize concretely the projective plane in R4 by choosing any parametrization of the sphere S2 and applying the map H to it. Actually, it turns out to be more convenient to use the map A defined such that
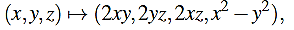
Because it yield snicer parametric zations. For example, using the stereographic representation where
Show that the following parametrization of the projective plane in R4 is obtained:
Investigate the surfaces in R3 obtained by dropping one of the four coordinates. Show that the re are only two of them (up to arigid motion).