Part a, b and c were already answered. I just need part (d) please
Attached the solution for the first 3 parts
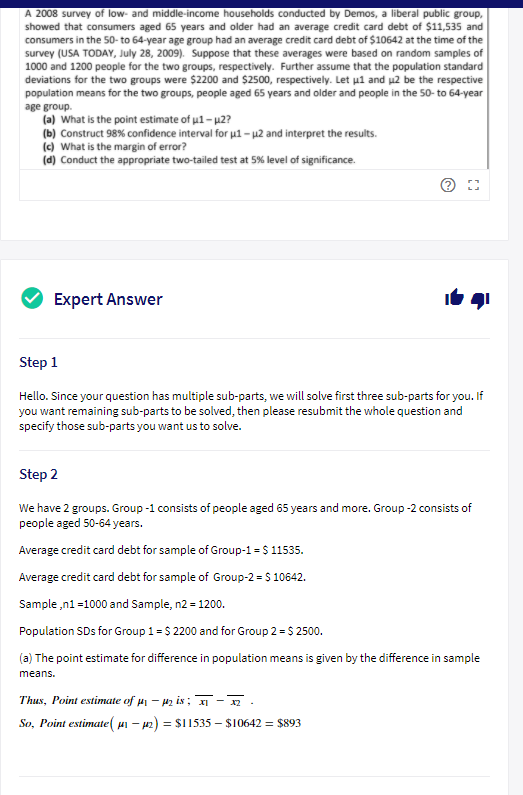
Extracted text: A 2008 survey of low- and middle-income households conducted by Demos, a liberal public group, showed that consumers aged 65 years and older had an average credit card debt of $11,535 and consumers in the 50- to 64-year age group had an average credit card debt of $10642 at the time of the survey (USA TODAY, July 28, 2009). Suppose that these averages were based on random samples of 1000 and 1200 people for the two groups, respectively. Further assume that the population standard deviations for the two groups were $2200 and $2500, respectively. Let ul and µ2 be the respective population means for the two groups, people aged 65 years and older and people in the 50- to 64-year age group. (a) What is the point estimate of u1- p2? (b) Construct 98% confidence interval for u1 – µ2 and interpret the results. (c) What is the margin of error? (d) Conduct the appropriate two-tailed test at 5% level of significance. Expert Answer Step 1 Hello. Since your question has multiple sub-parts, we will solve first three sub-parts for you. If you want remaining sub-parts to be solved, then please resubmit the whole question and specify those sub-parts you want us to solve. Step 2 We have 2 groups. Group -1 consists of people aged 65 years and more. Group -2 consists of people aged 50-64 years. Average credit card debt for sample of Group-1 = $ 11535. Average credit card debt for sample of Group-2 = S 10642. Sample ,n1 =1000 and Sample, n2 = 1200. Population SDs for Group 1 = $ 2200 and for Group 2 = $ 2500. (a) The point estimate for difference in population means is given by the difference in sample means. Thus, Point estimate of µ – 42 is ; -. So, Point estimate( ui – p2) = $I1535 – $10642 = $893
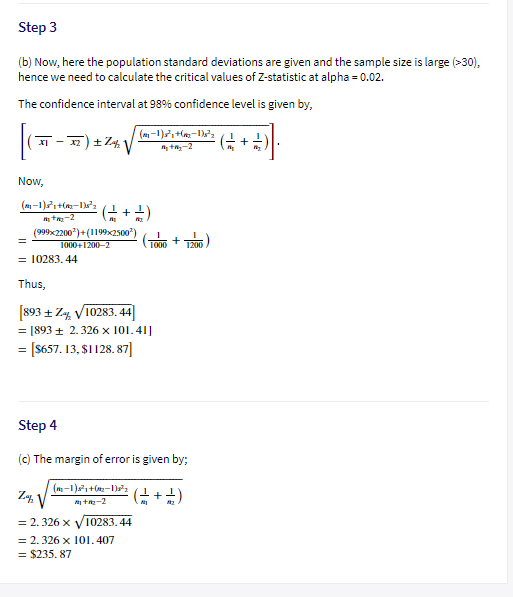
Extracted text: Step 3 (b) Now, here the population standard deviations are given and the sample size is large (>30), hence we need to calculate the critical values of Z-statistic at alpha = 0.02. The confidence interval at 98% confidence level is given by, tn-2 (부+ 부) Now, (-1)i+(-1'a (부+ ): t-2 (999x2200")+(1199x2500") 1000+1200-2 T200) 1000 = 10283. 44 Thus, [893 + Z% V10283.44 = [893 + 2.326 x 101.41] = [S657. 13, $1128. 87] Step 4 (c) The margin oferror is given by; (m-1)+(-1)2 Z% V (++) t-2 = 2. 326 x V10283. 44 = 2.326 x 101.407 = $235. 87