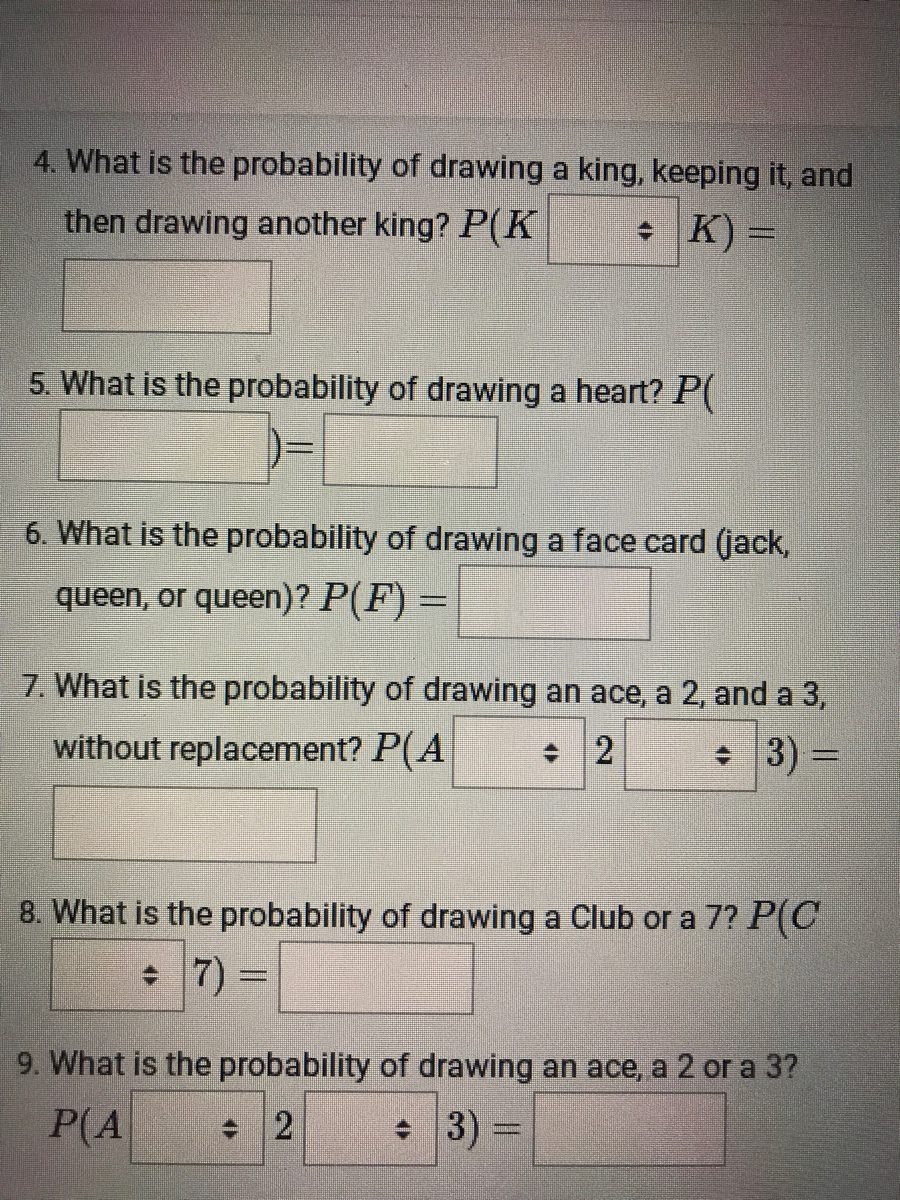
Extracted text: 4. What is the probability of drawing a king, keeping it, and then drawing another king? P(K * K) = 5. What is the probability of drawing a heart? P 6. What is the probability of drawing a face card (jack, queen, or queen)? P(F) = 7. What is the probability of drawing an ace, a 2, and a 3, without replacement? P(A * 3) = 8. What is the probability of drawing a Club or a 7? P(C + 7) 9. What is the probability of drawing an ace, a 2 or a 3? P(A 3) =

Extracted text: Problem 6: Now, find the following probabilities. Remember to ask yourself the questions, • Is this a simple or compound probability? • How many cards are being drawn? • Which conjunction is used and should we add or multiply? • If it is a compound probability, are the events dependent, independent, mutually exclusive, or not mutually exclusive? • Which formula should be used? Enter your answers as reduced fractions using / as the fraction bar. 1. What is the probability of drawing a king, replacing it, and then another king? P(K and K)%= 2. What is the probability of drawing a black or a red card? 3. What is the probability of drawing a red queen, keeping it, and then drawing a black queen? (P( + )= 4. What is the probability of drawing a king, keeping it, and then drawing another king? P(K + K) = %3D