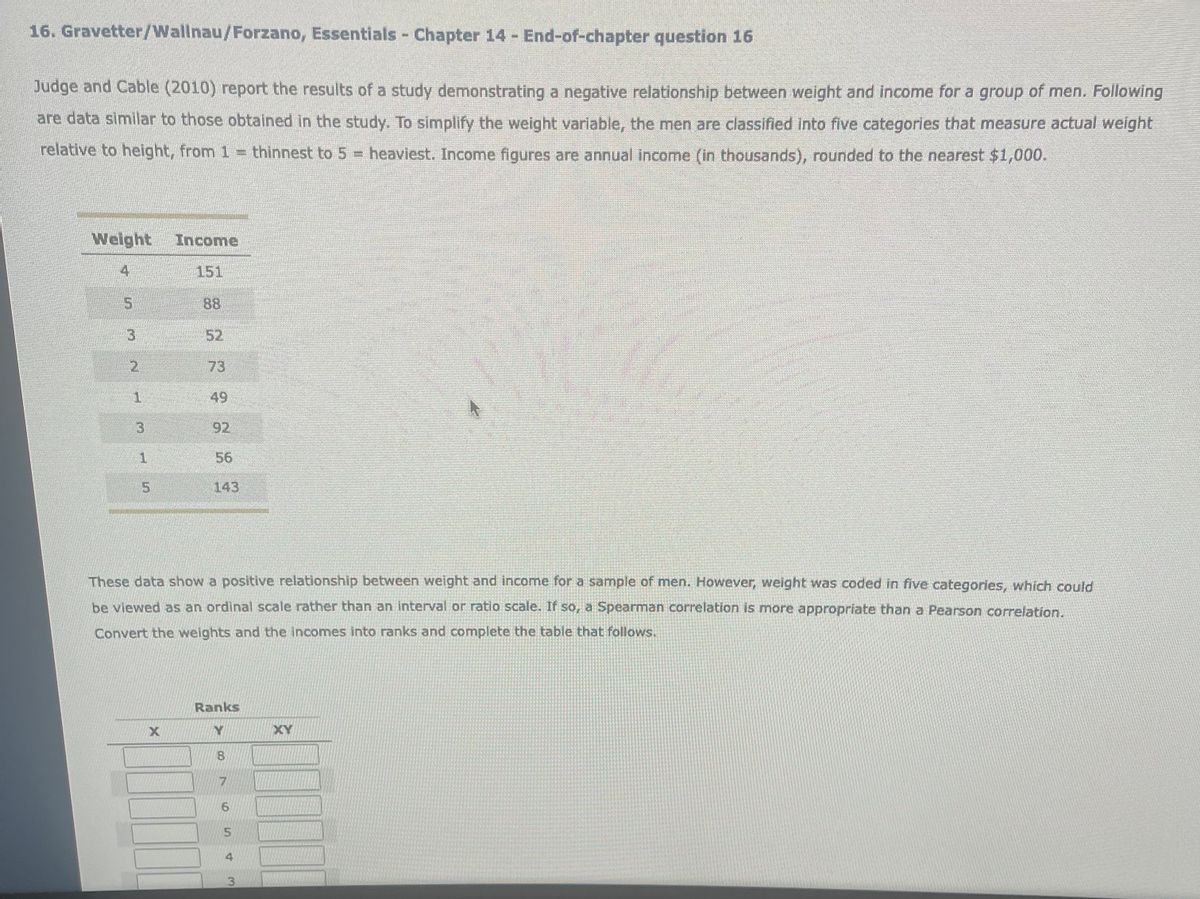
Extracted text: 16. Gravetter/Wallnau/Forzano, Essentials - Chapter 14- End-of-chapter question 16 Judge and Cable (2010) report the results of a study demonstrating a negative relationship between weight and income for a group of men. Following are data similar to those obtained in the study. To simplify the weight variable,, the men are classified into five categories that measure actual weight relative to height, from 1 = thinnest to 5 = heaviest. Income fiqures are annual income (in thousands), rounded to the nearest $1,000. Weight Income 4 151 88 3. 52 2. 73 49 92 1. 56 143 These data show a positive relationship between weight and income for a sample of men. However, weight was coded in five categories, which could be viewed as an ordinal scale rather than an interval or ratio scale. If so, a Spearman correlation is more appropriate than a Pearson correlation. Convert the weights and the incomes into ranks and complete the table that follows. Ranks XY
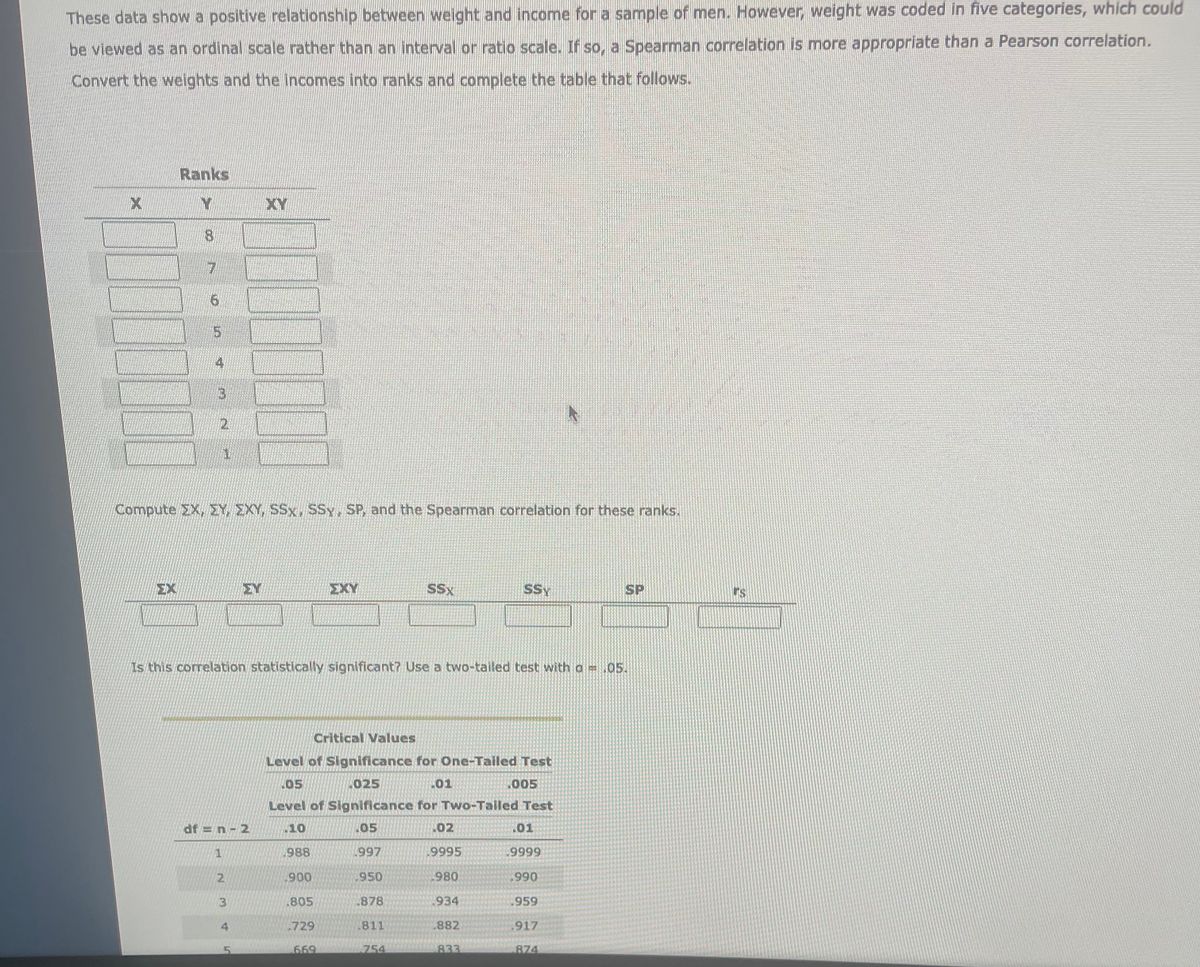
Extracted text: These data show a positive relationship between weight and income for a sample of men. However, weight was coded in five categories, which could be viewed as an ordinal scale rather than an interval or ratio scale. If so, a Spearman correlation is more appropriate than a Pearson correlation. Convert the weights and the incomes into ranks and complete the table that follows. Ranks XY 8. 5. 4 2. 1. Compute EX, EY, EXY, SSx, SSy, SP, and the Spearman correlation for these ranks. EX EY ΣΧΥ SSx SSY SP Is this correlation statistically significant? Use a two-tailed test with a =.05. Critical Values Level of Significance for One-Tailed Test 05 025 01 .005 Level of Significance for Two-Tailed Test df = n- 2 .10 .05 .02 .01 1 988 997 .9995 .9999 2 900 950 980 ,990 .805 .878 .934 .959 .729 .811 .882 ,917 669 754 833 874