I don't why al=(2n-1)pi/2. Can you please explain it to me?Thank you
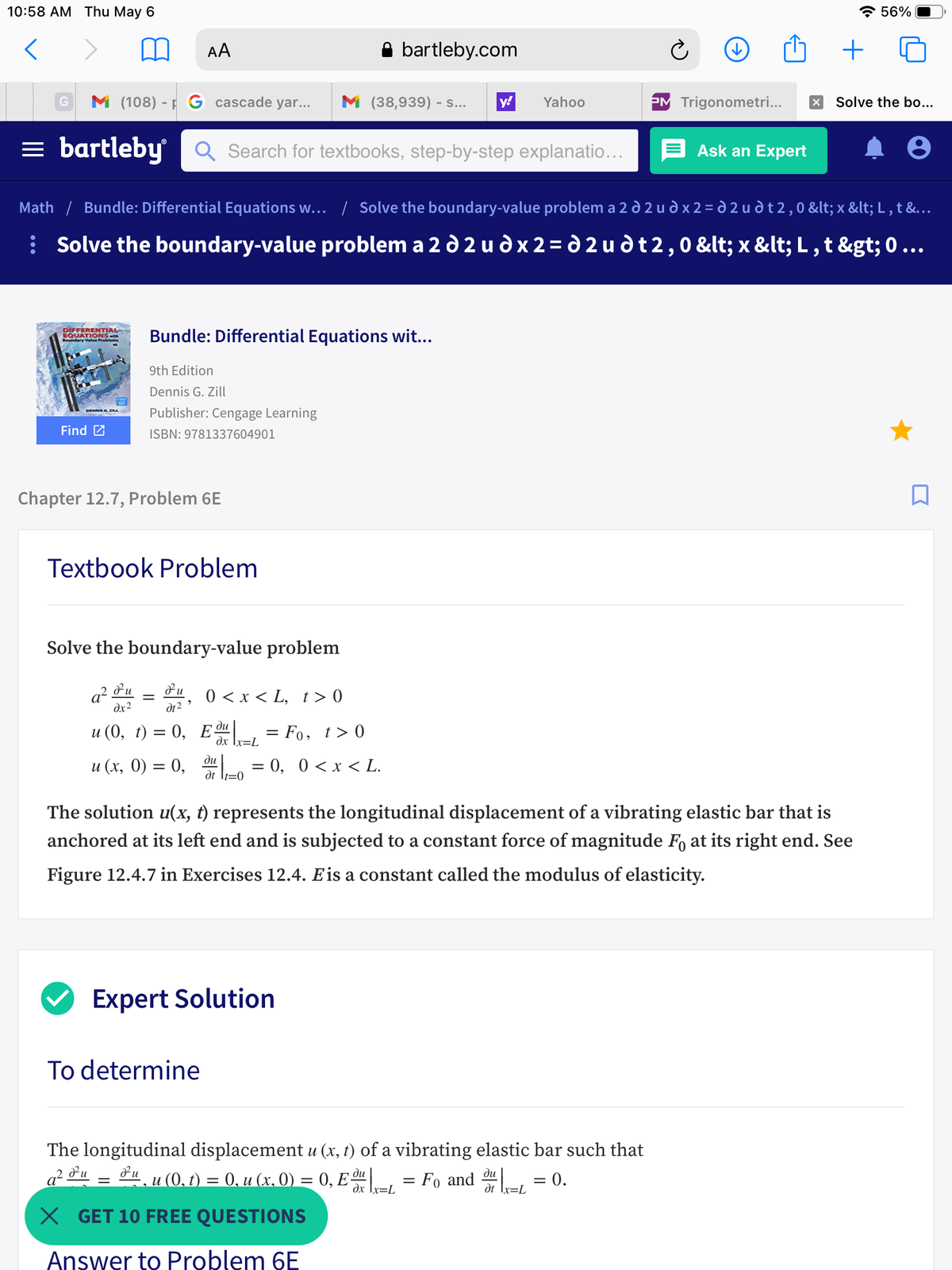
Extracted text: 10:58 АМ Тhu May 6 * 56% AA bartleby.com + M (108) - F G cascade yar... M (38,939) - s... y! Yahoo PM Trigonometri... Solve the bo... = bartleby Q Search for textbooks, step-by-step explanatio... Ask an Expert Math / Bundle: Differential Equations w... / Solve the boundary-value problem a 2 d 2 u d x 2 = d 2 u d t 2, 0 < x="">< l="" ,="" t="" &...="" |="" solve="" the="" boundary-value="" problem="" a="" 2="" d="" 2="" u="" d="" x="" 2="d" 2="" u="" dt2,0="">< x="">< l="" ,="" t=""> 0 ... DIFFERENTIAL EQUATIONS wth ndary Value Proo Bundle: Differential Equations wit... 9th Edition Dennis G. Zill Publisher: Cengage Learning DENNIS G ZILL Find 2 ISBN: 9781337604901 Chapter 12.7, Problem 6E Textbook Problem Solve the boundary-value problem a? dx2 0 < x="">< l,="" t=""> 0 || dt2 ди u (0, t) = 0, Eª = Fo, t> 0 dx [x=L ди и (х, 0) %3D 0, 0, 0 <х>< l.="" |f="0" the="" solution="" u(x,="" t)="" represents="" the="" longitudinal="" displacement="" of="" a="" vibrating="" elastic="" bar="" that="" is="" anchored="" at="" its="" left="" end="" and="" is="" subjected="" to="" a="" constant="" force="" of="" magnitude="" f,="" at="" its="" right="" end.="" see="" figure="" 12.4.7="" in="" exercises="" 12.4.="" eis="" a="" constant="" called="" the="" modulus="" of="" elasticity.="" expert="" solution="" to="" determine="" the="" longitudinal="" displacement="" u="" (x,="" t)="" of="" a="" vibrating="" elastic="" bar="" such="" that="" a²="" *u="&u_u" (0,1)="0," u="" (x.="" 0)="0," e="Fo" and="" l="0." dx="" ix="L" dt="" ix="L" x="" get="" 10="" free="" questions="" answer="" to="" problem="">

Extracted text: 10:58 АМ Тhu May 6 * 56% AA bartleby.com + M (108) - F G cascade yar... M (38,939) - s... y! Yahoo PM Trigonometri... Solve the bo... = bartleby Q Search for textbooks, step-by-step explanatio... Ask an Expert Math / Bundle: Differential Equations w... / Solve the boundary-value problem a 2 d 2 u d x 2 = d 2 u d t 2 , 0 < x="">< l="" ,="" t="" &...="" :="" solve="" the="" boundary-value="" problem="" a="" 2="" d="" 2="" u="" d="" x="" 2="d" 2="" u="" dt="" 2,0="">< x="">< l="" ,t=""> 0 ... X (x) = c8 sin (ax) (11) Differentiate the above equation with respect to x. X' (x) = ac6cos (ax) Substitute L for x in the above equation. X X' (L) = = ac8cos (aL) ac8cos (aL) = 0 (x' (L) = 0) (2n – 1) 5 (2n – 1) aL a = Therefore, the Eigen values are as follows An = an = ((2n – 1) ) Substitute the value of a in equation (11). X (x) = cg sin ((2n – 1) TX 2L The above equation represents the Eigen functions where. n = 1, 2, 3, .... Substitute a? for 1 in equation (6). T" + a²a?T = 0 The general solution of the above equation is as follows: T (t) = c9cos (aat) + c10sin (aat) (12) Differentiate the above equation with respect to t. T' (t) = -aac9 sin (aat) + aac10 cos (aat) Substitute 0 for t in the above equation. X GET 10 FREE QUESTIONS ) (T' (0) = 0)