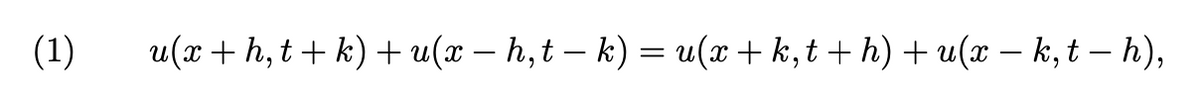
Extracted text: (1) u(r +h, t+ k) + u(x – h, t – k) = u(x+ k,t+ h) + u(x – k, t – h),

Extracted text: 2) Consider the initial boundary value problems: { Ə?u – au = 0, u(х, 0) — 0, u(0, t) = 0, πε (0, π ) ,t> 0, дли (и, 0) — 1, u(T, t) = 0, 6. x E (0, 7), initial data, t > 0, boundary values. %3D (a) Solve it using formula (1). (b) Is the resulting solution continuous? Is C1 i.e, u(, t) differentiable with d;u(x, t), dqu(x,t) continuous?