1. The geometric mean of the numbers 2, 4, and 8 is
we can compute G by logarithms or by using a calculator. For the geometric mean from grouped data,
2. The harmonic mean of the numbers 2, 4, and 8 is
For the harmonic mean from grouped data, .
3. The set 2, 4, 8 has arithmetic mean 4.67, geometric mean 4, and harmonic mean 3.43.
4. Use EXCEL to find Q1, Q2, Q3, D9, and P95 for the following sample of test scores:
88
|
45
|
53
|
86
|
33
|
86
|
85
|
30
|
89
|
53
|
41
|
96
|
56
|
38
|
62
|
71
|
51
|
86
|
68
|
29
|
28
|
47
|
33
|
37
|
25
|
36
|
33
|
94
|
73
|
46
|
42
|
34
|
79
|
72
|
88
|
99
|
82
|
62
|
57
|
42
|
28
|
55
|
67
|
62
|
60
|
96
|
61
|
57
|
75
|
93
|
34
|
75
|
53
|
32
|
28
|
73
|
51
|
69
|
91
|
35
|
To find the first quartile, put the data in the first 60 rows of column A of the EXCEL worksheet. Then give the command = PERCENTILE(A1:A60,0.25).
1. Write out the terms in each of the following indicated sums:
2. Express each of the following by using the summation notation:
(a) X2/1 + X2/2 + X2/3 +_ _ _+X2/10
(b) (X1 + Y1) + (X2 + Y2) + ___ + (X8 + Y8)
(c) f1X3 1 + f2X3 2 +_ _ _+f20X3 20
(d) a1b1 + a2b2 + a3b3 +_ _ _+aNbN
(e) f1 X1Y1 + f2X2Y2 + f3X3Y3 + f4X4Y4
3.
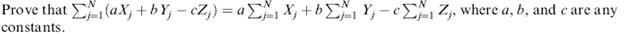
4. Two variables, X and Y, assume the values X1= 2, X1 = 2, X2 = -5, X3 = 4, X4 = -8 and Y1 = -3,