1. Let X =
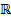
2
and define d2
:
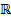
2
×
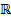
2
→
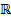
by
d2((x1, y1), (x2
, y2)) = max{| x1
− x2
|, | y1
− y2
|}.
(a) Verify that d2
is a metric on
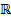
2.
(b) Draw the neighborhood N (0; 1) for d2, where 0 is the origin in
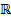
2.
2. Let X =
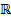
×
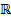
×
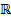
=
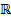
3
and define the metric d :
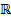
3
×
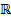
3
→
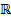
by
d((x1, y1, z1), (x2
, y2
, z2)) = max{| x1
− x2
|, | y1
− y2
|, | z1
− z2
|}.
Describe the neighborhood N (0; 1), where 0 is the origin in
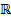
3.