1. Let X0
be uniformly distributed over [0, T], X1
be uniformly distributed over [0, X0] and, generally, Xi+1
be uniformly distributed over [0, Xi], i = 0, 1, ...
(1) Prove that the sequence {X0, X1, ...} is a supermartingale.
2. Let {X1, X2, ...} be a homogeneous discrete-time Markov chain with state space Z = {0, 1, ..., n} and transition probabilities
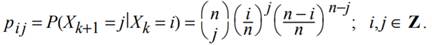
Show that {X1, X2, ...} is a martingale. (In genetics, this martingale is known as the Wright-Fisher model without mutation.)