1. A piston of area 0.1 m² sits atop a container filled with water as shown in figure below. A U- tube manometer is connected to the container at one end. The other end is open to the atmosphere. If...

kindly help me with this problem I provide some information for the solution needed.

Use free floating decimals in all your calculations and in expressing your final answers.
• Solve problem SYSTEMATICALLY and NEATLY thank you!

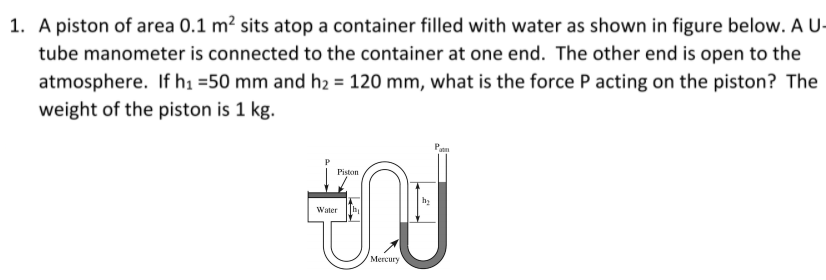
Extracted text: 1. A piston of area 0.1 m² sits atop a container filled with water as shown in figure below. A U- tube manometer is connected to the container at one end. The other end is open to the atmosphere. If h1 =50 mm and h2 = 120 mm, what is the force P acting on the piston? The weight of the piston is 1 kg. Piston Water Mercury


Extracted text: A U-tube manometer is shown in the Figure above. The pressure P, is exerted on one arm of the U-tube and P, on the other arm. Both pressures P, and P, could 1. Differential Manometer (Multiplying Gauge) In this device, the end of a U-tube are connected to two enlarge chambers. The manometer contains two liquids B and C which are immiscible , and whose densities are as nearly egual as possible. The closer the densities of the two liquids, the more sensitive is the manometer. be pressure taps from a fluid meter, or P, could be a pressure tap and P, the atmospheric pressure. The top of the manometer is filled with liquid B, having a density of p.and the bottom with a more dense fluid A, having a density of e,. PB Liquid A is immiscible with B. Derive the relationship between P, and P,. Using point 2 and point 3 as our reference since both points lie on the same liquid level (b) P = P, P. + Pg (Z+R)= P, + Pg g. P.- P, = (R-Ro) [ pa – po + (a/A) ps – (a/A) pc ] g. P. - P, = P. Z+ P. R- P, 3 (Z + R) ge ge Where: R= actual reading ge Ro = reading when Pa = P. P. - P, = PA 8 R- PB g. ge Derivation of Inclined Manometer Equation: b. Inclined Manometer - this is often used for the measurement of small opposite side Rm Rm = R1sin a R1 sin a = pressure differentials accurately. Used to measure very small pressure differences or changes It is slant manometer. The angle of measuring leg is usually about 10°. • Inclination is done to improve the sensitivity. It measures more accurately than the vertical tube type manometer. һуpotenuse P1 = P2 Pa + Pa OB2)Rm = Pg + PA Rm PA + Pa2)R1sin a = Pg + Pa R, sin a Pressure Pressure PA - Pg = PA (2)R, sin a- pe Po()R,sin a P. P. INCLINED MANOMETER PA - Pg = (Pa – PB)2)R15 sin a EQUATION opposite side Rm sin a = hypotenuse R1